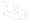Tutorial: Music theory basics
This is an introduction to music theory. It will be mostly aimed at guitar players, but the theory will be true across all musical instruments. The goal of this document is to provide a basic understanding of music theory and ways to apply this theory with practical examples.
Part 1: notes, keys and scales
To start off this introduction, we will begin with the fundamental basics. And for that, we need a short excursion into the realm of physics.
What is a note?
A single note we play on a musical instrument has an incredibly large number of properties. It can be high or low, loud or soft, long or short. It has a certain timbre (how it sounds) or certain "effects" applied to it like a vibrato or pitch shift. For this music theory course, we will focus on one single thing: the pitch of the note. In other words, how high or low the note is.
Let's imagine a piano. It has a lot of keys that can be tapped to play individual notes. All the way to the left side of the piano are the lowest notes. As you go to the keys further to the right, the pitch of the notes will increase. The notes become higher. For guitar players, the same is more or less true. Pluck an open string and you get a lower note than when you finger that string higher up the neck and play that note.
Most people will probably be aware that we assign letters to notes to indicate what their pitch is: A, B, C, D, E, F and G. After G, we don't go to H but we go back to A. Why is this? To answer this we first need to learn what determines the pitch of a note.
A note is sound. But what is sound? Sound is vibration. When we pluck a string on the guitar it starts to vibrate. The vibrating string makes the air around it vibrate as well. This vibration continues through the air and at some point it reaches your ear. Inside your ear there is a thin membrane called the eardrum. The vibrating air causes the eardrum to vibrate and that is experienced as sound.
When we pluck a string on the guitar, the speed of the vibration determines the pitch of the tone. When we play a higher tone, the string vibrates faster than when we play a lower tone on that same string. The speed of this vibration is called the vibration frequency. This is simply the number of times the string will vibrate up and down in one second. We express the frequency in hertz (hz). 440hz means 440 vibrations per second. The faster a string vibrates, the higher the frequency and the higher the pitch of the note.
Each of the letters A to G have been assigned to specific frequencies. Different cultures in different parts of the world use different frequency assignments. Modern western (pop) music uses what's referred to as "concert pitch" (made official through the ISO 16 standard), where the A (or more accurately, the A4 or "middle A", which is the 5th fret on the high E string on a guitar) is assigned to 440hz. The notes around that have been assigned to higher (or lower) frequencies.
I referred to the 440hz A note as the A4, because as is defined by the concert pitch standard, there are also A0, A1, A2, A3, A5, A6, A7 and A8 notes. The frequency of each of these A notes doubles as you go to a higher A. For instance, the A4 has a frequency of 440hz and the A5 has a frequency of 880hz. Similarly, the A3 has a frequency of 220hz. The same is true for all of the notes. The C4 is pitched at 261.6hz while the C5 is pitched at 523.2hz (which is twice as much). This is why we define only A to G, as the next note after G will be a doubling of the (frequency of the) previous A.
This is the underlying mathmatical principle. What we as musicians need to understand is that going from an A to the next A is called an "octave". Or more accurately, the difference between two notes with the same name is an octave. Going from a C to the next C is an octave. Going from an F to the next F is an octave as well. In musical terms, we call the difference between two notes an interval.
Sharps and flats
A, B, C, D, E, F, G... we aren't there yet. These seven notes represent the white keys as found on a piano. But there are also black keys on a piano. These are the notes inbetween the seven notes in an octave. For instance, between the A and B, there is also the A sharp, commonly written as A♯. Between the C and the D, there is the C sharp (C♯). Between D and E there is the D sharp (D♯). And so on. When we add these half-step notes, we get the complete set of 12 notes that exist in our western musical system: A, A♯, B, C, C♯, D, D♯, E, F, F♯, G, G♯. This is commonly referred to as the chromatic scale.
The attentive reader will have noticed that there are sharp notes between each of the whole notes, except for the B-C and E-F intervals. The reason for this is that the interval between each of the 12 notes listed above is half a step (also called a semi-tone) and the interval between a B and a C is already just half a step. The same is true for the interval between the E and F. So there is no such thing as a B♯ or an E♯ in our western chromatic scale.
There's also such a thing as a flat note. This is basically the opposite thing of a sharp note. Whereas a sharp note increases the note by a semi-tone, a flat decreases the note by a semi-tone. We write a flat tone by suffixing a ♭ to the note: A♭, B♭, D♭, E♭, G♭. Bluntly speaking, this means an A♭ is the same as a G♯, a B♭ is the same as an A♯, a D♭ is the same as a C♯, etc. Again, we do not have a C♭ or F♭ because the B-C and E-F intervals already are semi-tones. When we use sharps and when we use flats is something that will be discussed later on. For now, we'll stick to sharps.
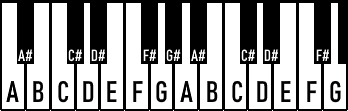
All chromatic notes on a piano